The trike moves forward! This seems counterintuitive to almost everyone (certainly it is to us), but the result of an experiment with a real trike is indeed that it moves forward.

You can check it out - just find a trike. You do have to be careful not to let that front wheel twist sideways. You need to do something to keep it from twisting, but without pushing forward or backward on it. You can gently put a finger against the side of the wheel. Or you could use duct tape (the all-purpose American solution to all problems) to, say, strap the wheel's fender to the main frame of the trike. Or you can use a bicycle instead of a tricycle, but then you have to gently use your fingers to keep it from flopping over sideways.

Here is our trike. (Thanks to Ted Romer for "loaning" us his trike. He doesn't use it very much any more, anyhow, and we needed it more than he did. We made an extension to raise the handlebars so that we could ride it if we wanted to, but remember: In this "pushing the trike" experiment, you do not ride the trike, instead you stand or kneel next to it and push on that pedal.)

You can see that we made a wooden brace between the front fender and the rest of the trike, to keep the front wheel from twisting, but you don't need to be that elaborate.

And you must remember to push gently forward on the pedal that is initially pointing straight down:

Here's an analysis of the trike problem, which (if you do it very carefully) is actually a fairly stiff first-year physics problem. The trike starts at rest, we will apply a force to the pedal, and we want to know which way it will start to move. (After it's moved a bit, the pedal will no longer be directly down. We won't worry about that - just concentrate on its velocity right after it starts to move.) Forces cause accelerations, and since it starts at rest, its initial acceleration will be in the same direction as the direction of its velocity an instant after the beginning of our experiment. So what we want to know is the direction of its initial acceleration.

The important parts of the trike are the front wheel and the pedals. You can think of the rest of the trike as superfluous stuff that is dragged along behind and keeps the whole trike from tipping over. (If you're planning to use a bike for your experiment, think about the pedals, the chain, and the rear wheel, and ignore the rest of the bike.)

In thinking about this problem, the absolutely essential thing to remember is that you are NOT riding on the trike - you are standing next to it and pushing. If it were not an actual trike but just a similarly behaving piece of physics department demonstration apparatus that behaved like a trike, then probably most people wouldn't guess the wrong answer. (They would be more likely to say: "I don't know, let's ask the teacher". What we hope they would say is either "Let me think about it" or "Let's try it, where's my trike?") It's because we have all ridden on trikes and (we think) know everything there is to know about trikes that most of us just jump to the erroneous conclusion: Push forward on that lower pedal and "of course" the trike will go backward. (Like the big guy in the second panel of the bus placard: "I've known about trikes since I was two.")

For starters, here's a semi-intuitive way of looking at the trike problem. Look down to the diagram below. That F represents the forward push of your hand (to the right in all these diagrams). Forget the other symbols in that diagram for now. Since the pedal is rigidly attached to the front wheel, it's really just part of the wheel, providing a convenient place for you to push. Now the force F tends to rotate that wheel clockwise around the point of contact between the wheel and the ground (the point directly below the center of the wheel). And if the wheel does start to turn clockwise, then the wheel will have to move to the right, forward. End of story.

Physicists hate to depend on wishy-washy terms like "tends to ...", so we find that description rather unsatisfying. Below is a thorough treatment, complete with torques, equations, etc. Nevertheless, the "semi-intuitive" version given above is a pretty good summary of "why" the trike moves forward when you push forward, as good as it gets if you want to avoid the equations and the technical terms. Way down below, under the heading "Alternative Theory", we give a beefed-up treatment (with equations!) of the initial "semi-intuitive" version given just above.

Now for the physicists' version:

Let the radius of the wheel be R and the length of the pedal arm be r. We apply a force (call it F) on the pedal in the forward direction. Now the ground will probably also exert a force in the horizontal direction (call it f, it's really a "frictional" force), but we don't know to begin with whether f is in the forward or backward direction. Let's take the positive direction to be forward and let F and f denote the components of those forces in the forward direction. (If f turns out to be negative, then that simply means that f, a vector, is in fact in the backward direction.) There are also forces (up and down) in the vertical direction, exerted by the earth's gravity and also the upward push of the ground, but we'll leave those out of our analysis because we only care about the horizontal motion.

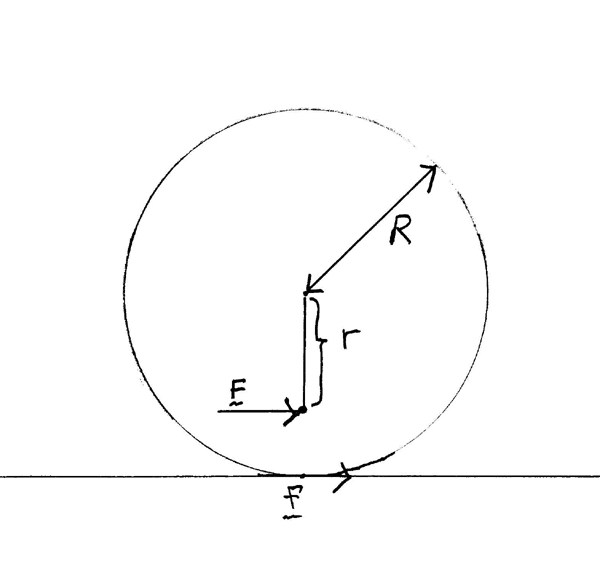
Newton's second law gives

        F + f = ma      (1)

where m is the mass and a is the component of the acceleration in the forward direction. We want a, but f in Eq. (1) is unknown. We need more physics, which we can get from the torque equation.

As drawn, both F and f produce torques tending to turn the wheel counterclockwise. (That is, counterclockwise around its axle, the center of the wheel. That's what "clockwise" or "counterclockwise" refer to in this discussion. By contrast, in the initial "semi-intuitive" discussion given earlier, that force F tends to turn the wheel clockwise with respect to the contact point with the ground, and f exerts no turning effect at all with respect to that contact point.)

Care with signs is essential here. Let a denote the angular acceleration in the clockwise direction. Then a and a are related by

a = a/R     (2)

and the torque equation (get the signs right!) is:

      Fr + fR = - Ia       (3)

where I is the moment of inertia about the center of the wheel.

Now comes a little algebra (which we'll omit), leading to the results:

      a = FR(R - r)/(I + mR² )         (4)

(That last term in parentheses in (4) is supposed to be m x R x R, i.e., mass times the square of the radius. On some browsers, what should be a superscript "2" shows up as a "?" (question mark). Similar peculiarities may show up in several of the equations below. Ah, the idiosyncrasies of computers!)

All that we care about is the sign of a. Since R > r (the radius of the wheel is greater than the length of the pedal arm), a is positive - the trike moves forward.

That surely is contrary to most people's "intuition", probably because we have all ridden trikes and we know that the way to back up is to push forward on the pedal that is pointing down. Remember, though, that in our problem, we are not sitting on the trike, instead we're standing next to it. Those are two different situations, and there is no reason to expect their solutions to be the same.

It's still strange, though, to see the trike move as it does. As you push forward on the downward pointing pedal, the trike really does move forward a bit and that pedal rises up. Here are two sketches of trike-plus-pedal - first when it's at rest, and then when it has moved a bit.

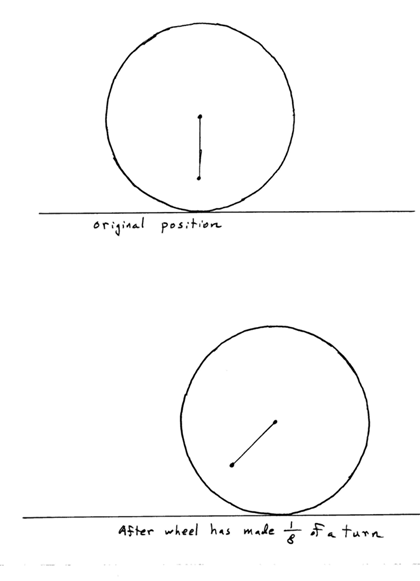
The wheel as a whole moves forward. So does the pedal. Relative to the wheel, it's true that the pedal moves backward. That is, though the wheel and pedal both move forward, the pedal doesn't move quite as far forward as the wheel does. Another comment - These sketches only show the front wheel and one of the pedals, not the rest of the trike (seat, handlebars, etc.) But look at the center of the wheel. Notice that although the wheel turns and the pedal turns with it, the center of the wheel definitely moves forward. And if the center of the wheel moves forward, then so does all the rest of the trike - seat, frame, handlebars, etc.

You can also solve equations 1-3 for f, which gives:

         f = - F(I + mRr)/(I + mR²)            (5)

Notice that f is definitely negative. That is, the frictional force always is in the backward direction. Thus the frictional force, if it acted alone, would indeed push the trike backward. But in our case, as long as R > r, f is not large enough to offset the force that we exert, F. (Look at Eq. (5). If R > r, then the size of all that stuff multiplying F on the righthand side of the equation is less than 1, so Eq. (5) tells us that the magnitude of f is less than the magnitude of F.)

What if r were greater than or equal to R? That is what if the length of the pedal arm were as large as the radius of the wheel or even greater? Eq. (4) says that if r = R, then a =0, and the wheel won't move. And that equation also says that if r > R, then a < 0, that is, that the trike will indeed movebackward.

Normally, you can't have r that large, but you can achieve that condition by putting an extension on the pedal and then resting the whole thing at the edge of a table, so that the “pedal” is down below the edge of the table:

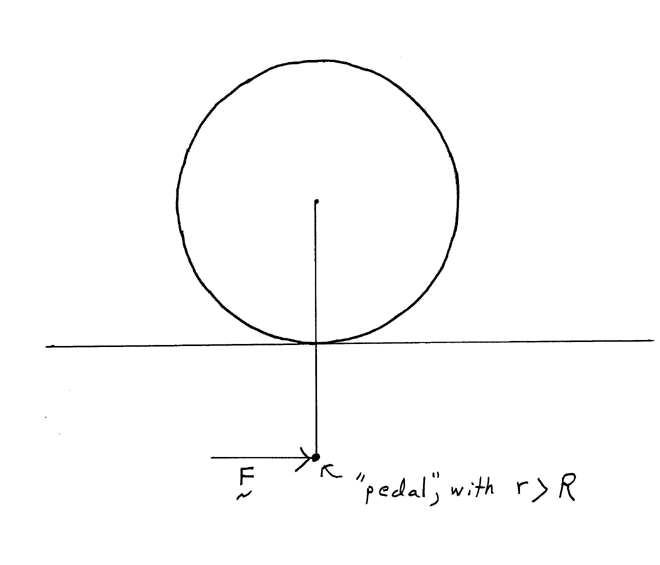
Now if you push forward just at the edge of the table ( r = R ), you'll find that the trike won't budge - until you push it so hard that it begins to skid, without rolling. (We assumed rolling in our analysis of the problem, so our theory can't be expected to make any sense if it skids.) And if you apply your forward force down below the edge of the table (r>R), as in the sketch just above, you'll find that the trike does begin to move backward.

Alternative Theory:

(This is a careful version of the initial discussion given at the beginning, what we called the "semi-intuitive" version.) In the preceding analysis, we calculated torques about the center of mass. It is also legitimate to take torques about any fixed point, if we're careful, and sometimes it's simpler to do so. Taking torques about the point in the ground where the wheel touches the ground, we have:

         F(R - r) = I’a      (6)

where I’ is the moment of inertia with respect to that new point. By the principal axis theorem (from introductory physics),

      I’ = I + mR² ,

and, with this alternative theory, a is still equal to a/R.

Putting those results into Eq. (6) leads to the same expression as before for a, Eq. (4). This approach is algebraically much simpler. We don't have to introduce f, since it exerts zero torque about that point in the ground. Although this approach is simpler and more elegant, it may seem a bit too simple to be reliable, and it's reassuring to know that we can also get the same result by our first approach, calculating torques about the center of mass. And part of the fun of doing physics is that often there are several different and equally correct ways of tackling the same problem.

Return to bus placard

Return to main menu