Of course the basic reason that things look different in the passenger-side mirror, not the way they do when you look at them directly, is that the surface of the mirror is curved. If you feel it with your hand, you can almost feel that it is a convex surface. A sure-fire way to tell is to take something straight, e.g., a 3" x 5" index card held edgewise or a 6" ruler, and hold it against the mirror; you can easily see from this that the mirror is by no means flat. If you have someone hold a little flat mirror next to that mirror, then by comparing what you see in the two mirrors, you can see that indeed things do look smaller (and thus as if they are farther away than they really are) in the curved mirror. And a handy convex mirror to experiment with is a spoon: hold it with the bottom of the spoon facing toward you and look at your reflection in the spoon. Almost everyone has looked at reflections in curved mirrors, especially concave mirrors, for instance the type that are found in many bathrooms for giving you a closeup look at your face.
(Many people naturally wonder why the automobile manufacturers don't make the passenger-side mirror flat and avoid the distortion (and the risk involved in having it seem that that truck is farther behind you than it really is). Is it just perversity out in Detroit? No, it's because if that mirror were flat (and that's the way the first passenger-side mirrors were), you couldn't see as much of what is behind you. The "field of view" would be smaller, and that would pose a larger risk than would the misleading sense of distance that you get from a convex mirror. As long as the driver is aware of the fact that objects as seen in the mirror are really closer than they look, it's safer to choose the larger field of view.)
For more quantitative experiments, you can buy a replacement passenger-side mirror for your car, but it will cost quite a bit. We suggest instead going to the automotive section of a big store (probably at the mall) and buying a small "stick-on" convex mirror for 2 or 3 dollars.
To be sure, the light that reaches the driver's eyes from the passenger-side mirror does have to go a little bit farther to get to her eyes than does light from the driver's-side mirror. And so things seen in the passenger-side mirror would look a tiny bit smaller, even if that mirror were flat. But the extra distance is only a foot or so, and if you're looking at a truck 70 feet or so behind you, a couple of feet more or less would only make an extremely small change in the apparent size of that truck. By itself, that slight extra distance can't be the explanation. Besides, all you have to do to test that idea is to stop the car, undo your seat belt, and move over into the passenger seat - things seen in that mirror still look farther away than they really are.
We'll see later, though, that there is just a germ of truth in the silly remark
that things look smaller than they really are because the light has to go
farther to get to your eye; the amount of reduction in size does turn out
to depend on how far away from a curved mirror your eye is.
How
to work it out? The important factor determining how big an object looks is
the angle it "subtends" at your eye. In the case of a truck
behind you on the highway, let's take this to be the angle between two light
rays coming to your eye, one from the bottom of the truck, the other from
the top. If the truck is 8 feet high and is 4 car lengths (about 70 feet)
behind you, the angle (if you look at it directly - or in a flat mirror, for
that matter) is about 8/70 = 0.1 (in radians, which is about 7 degrees). Almost
all the angles we deal with in this problem are small, and we use "small
angle approximations" because it simplifies the math. We will usually
express angles in radians, and 10% accuracy is fine for this problem.
Here's
a sketch (not to scale!) of a truck behind you, a convex mirror, and
your eye. You see light from all of the truck, but the sketch simply shows
two rays of light, one from the bottom of the truck and one from the top,
both of which are reflected from the mirror and arrive at your eye. 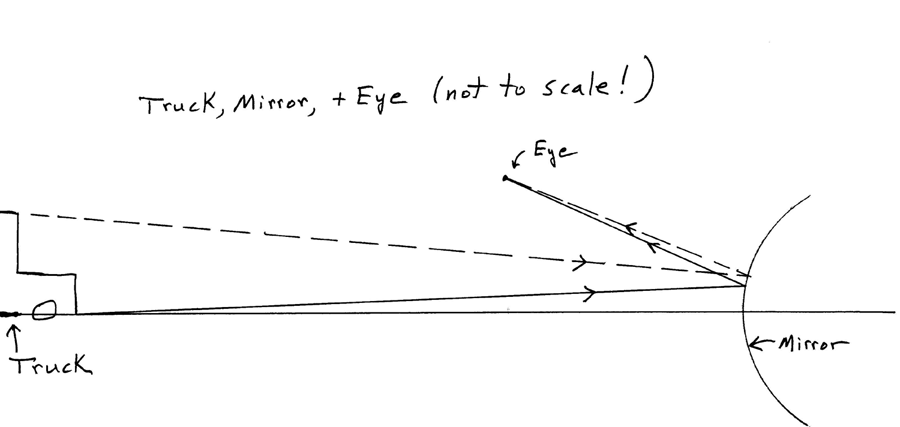
There
are plenty of other rays, but the others from the top and bottom of the truck
miss your eye. (We're treating the eye as if it were very small - which it is,
in this context.) And we don't show any of the light coming from intermediate
points, such as the radiatior cap, etc. Light reflects from a curved
mirror just as it would from a small flat mirror that is tangent to the
curved mirror at the point where the light reflects. "Locally", the
curved mirror acts no differently from a small flat mirror. Both of the rays
shown are drawn so that they follow the usual rule of reflection: angle of incidence
= angle of reflection. That's the only basic physics involved here -
though being careful about applying this physics and thinking about what angles
are important, etc. is also an important part of the practice of physics.
From
the sketch, it certainly looks as though the angle between the two rays coming
to your eye from the top and the bottom of the truck is indeed quite small,
smaller than the angle you would get by looking directly at the truck. To get
quantitative about this, it is useful to introduce some of the formalism of
geometrical optics. A convex mirror like this has a "focal length"
(f) , which is equal to R/2, where R is the radius of curvature of the mirror.
(When we say that the focal length is f, we mean that a very distant object
will form a "virtual image" at about a distance f behind the surface
of the mirror.) You can measure the
radius of curvature of such a mirror by putting a short straight ruler across
it, measuring the distances shown in the following sketch, and doing a little
geometry. (We are only after approximate results, so there is no need to be
fussy. Approximate! For instance, don't worry about whether you measure the
distance x the way it's shown
(perpendicular to the ruler) or instead perpendicular to the mirror surface.)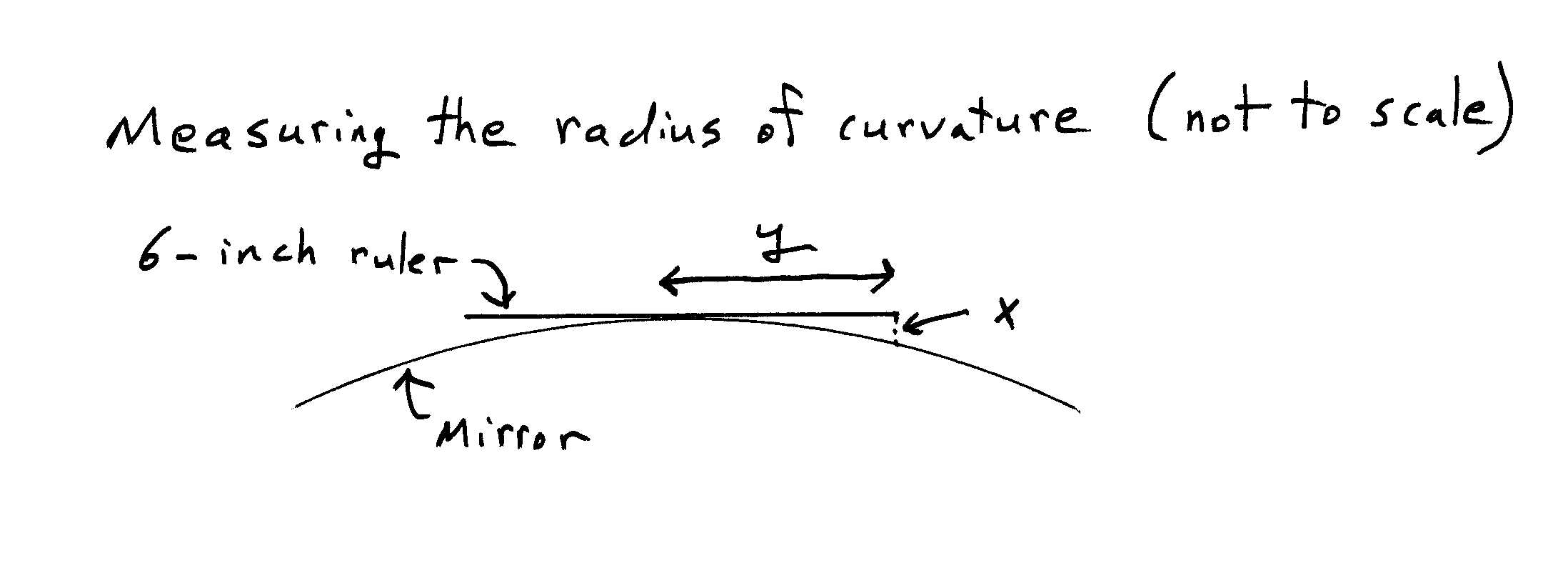
For
the passenger-side mirror on a 2000 Chevy Prizm, with y = 3" (we used a 6”
ruler), we found x to be about 2 millimeters (sorry about the mixed units), and
then some geometry and conversion of units leads to the conclusion that R is
about 56” (and so f is about 28” = 2.3’).
If
we're looking at a truck behind us, then the distance to the truck (call that
distance s) is surely >> f. And the size of the image (say its
height, h) is less than the actual height of the truck (H) approximately by
the ratio of the distance s to the distance f:
h/H
= f/s.
(It
takes some drawing of light rays and work with similar triangles to work out
that result.)
If
f = 2.3' and s is, say 70’, then h is much smaller than H. But the
image of the truck is much closer than the real truck, and what really
matters is how large an angle there is between the light coming to
us from the top of the truck and the light from the bottom of the truck. Call
that angle A for the case where we're looking directly at the truck. A is
surely small enough so that small angle approximations are OK, so
A
= H/s
With
the numbers used earlier, A = 8/70 =
0.1 radians.
Call
A' the angle when we're looking at the image, which has a height h. The
image is a distance f behind the mirror, so its distance from our eye is (E +
f), where E is the distance from our eye to the surface of the mirror, and so:
A'
= h/(E + f) = Hf/s(E + f)
and
what we really care about is the "magnification" (M), the ratio of
those two angles:
M
= A'/A = f/(E + f).
M
is obviously less than 1 (things do look smaller), but we still call it the
"magnification". So M depends on two things: the focal length (and
thus the amount of curvature of the mirror) and the distance from the driver's
eyes to the mirror. For the driver of our Prizm, E is about 4.2’, and so for
her (we’ll leave out a bit of arithmetic – you can fill it in), M is about
0.36, which seems reasonable. That is, this is roughly what one's subjective
sense is of how much smaller and farther away things appear in that mirror.
This
is our main result. For the driver, M is around 0.3 or 0.4, definitely less
than 1, but not enormously smaller, not down around 0.1 or anything like that.
The
passenger, though, is closer to the mirror. For him, E is only about
1.8’, which makes M about 0.56.